
Advanced Research Group
ご興味・ご関心ございましたら、こちらから
新着記事
IMAGICA GROUP の ARG (Advanced Research Group) とオー・エル・エム・デジタルは、2019年からニュージーランドの首都ウェリントンにあるビクトリア大学と連携し、CGに関する最先端技術調査や共同研究を実施してまいりました。
本手法は、ポリゴンモデルの特徴領域を抽出・保持し、高速なポリゴンリダクションを可能とするもので、上記共同研究の成果の一つです。もともとビクトリア大学が推進していたポリゴン削減のための特徴領域抽出技術に着目し、グループの関連会社内での実証実験などをもとに改良を加え、2023年1月に国際論文誌に採択されました。
まずその研究成果をご覧ください。図1(左)が1400万頂点のオリジナルモデル。同図(右)は本手法によって1/100の頂点数に削減した結果です。目の周りの凹みや、唇、足の指の間の隙間など、顕著な特徴領域を保持できています。

図1 1400万頂点からなるオリジナルポリゴンモデル(左) と本手法によるポリゴン削減結果(右).頂点数は
1/100 以下になっている.
では、この技術について背景から詳しく説明します。
点群データなどをもとに、3Dオブジェクトの複雑で高密度なポリゴンモデルを用いることは今や必要不可欠です。ゲームなどのリアルタイム応用やシミュレーションと組み合わせるエンジニアリング応用などを想定しますと、もともとの高精細モデルが捉えた複雑で特徴的な領域は保持しつつ、全体としては大幅にポリゴン数を減らせる手法が切望されています。もちろん高速処理でこれを実現したいわけです。
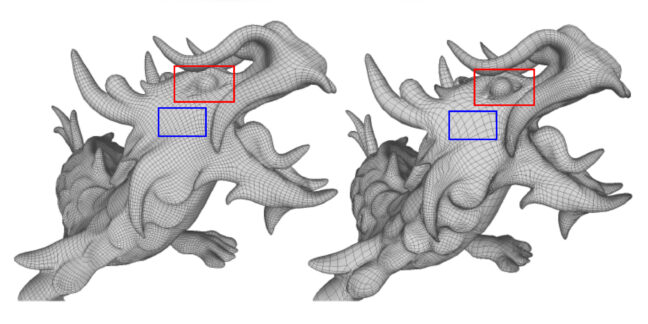 図2 市販ツールによるドラゴンモデルのポリゴン削減結果(左) と、本手法による結果(右).
図2 市販ツールによるドラゴンモデルのポリゴン削減結果(左) と、本手法による結果(右).
しかしながら既存の市販ツールではこうした要求を満たせるものはありません。図2(左) に従来手法によるポリゴン削減結果を示しています。この図の赤と青の囲みからもわかるように、全体的に均一に削減されています。このときアーティストはポリゴン削減率のみを指定し、削減プロセスそのものを制御していません。重要なところもそうでないところも一定の比率で削減されてしまうので、形状の特徴となる詳細部分までもが削られてしまいます。同図(右) では本手法によるポリゴン削減結果を示しています。同図(左) と比べて、ドラゴンの頬のあたりはより粗く、また目の周りはより細かなポリゴンで表現されているのがわかります。
アーティストにとって大事なディテールは細かいまま残しつつ、ポリゴン数は大幅かつ高速に削減したい” という目標に対し、これを実現するために次の3つの技術課題を設定しました。
(1) Robustness: 高精細モデルに対する計算の安定性
(2) Efficiency: 大規模計算の高速処理
(3) Good GUI: 使いやすいパラメータ制御
では、本手法をもう少し詳しくみていきましょう。
そもそも “複雑で特徴的な” ディテールをどう定義するか? を考える必要があります。これについては既存研究がいくつかありますが、本手法で採用したのはエントロピーを用いる方法です(例えば[1]や[2]. 日本語の簡単な解説は[4]にあります):
ここでいうエントロピー、もう少し正確には情報エントロピーですが、ポリゴンの各頂点について定義される量です。その点の近傍でどの程度幾何学的に複雑な情報をもつかを(確率論的に平均情報量として)定義するものです。各頂点の近傍のスケールを数段階に分け、そのスケールに応じて幾何学的な情報のエントロピーを調べました。例えば 従来研究[1]ではこの幾何学的情報として、ガウス曲率や平均曲率を用いました。
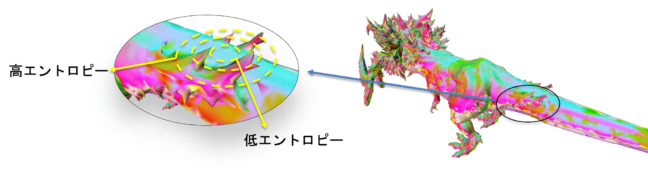
図3 エントロピーの計算. エントロピーは確率をもとに計算されるが、対象となる頂点の近傍の大きさに応じた幾何学的量(通常は曲率) の頻度分布として確率を定義する.
しかし我々の取り扱うような大規模なポリゴンモデル(例えば頂点数が数百万以上)に適用すると計算が不安定となったり、計算時間が数時間以上になるため、実用的でないことがわかりました。そこで次の方針をとりました。
本手法では、各頂点の近くでのポリゴンモデルの曲がり具合(curviness) を、新しく定義した疑似的曲率で測ります。まず図4を用いて平面上の曲線の曲率の定義を復習してみます。
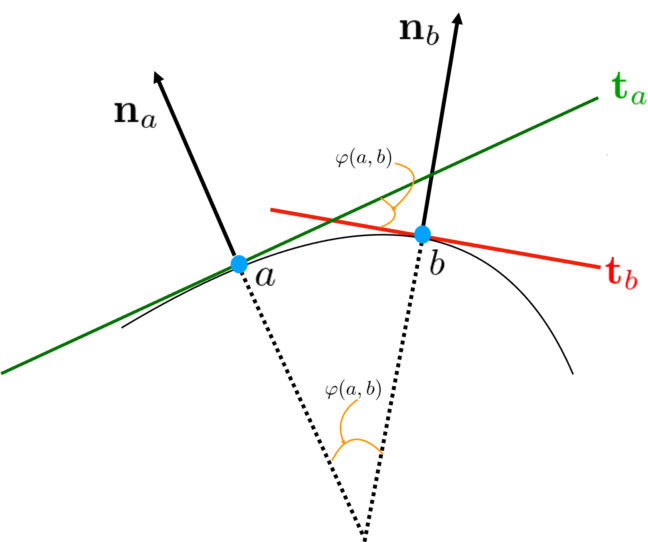
図4 曲率の考え方
同図において、平面上の点 a と点 b を通る曲線について考えます。ここで ta と tb はそれぞれ点 a と点 b におけるこの曲線の接線を表します。 na と nb はそれぞれ大きさが 1で ta と tb に垂直な方向ベクトルを示します。 na と nb のなす角度を φ (a, b)と記せば、 点 a におけるこの曲線の曲率を κ(a) と記しますと、κ(a) の絶対値はだいたい φ (a, b)×(孤 ab の長さ) になります。したがって曲線上の点をサンプリングするときに等間隔でとれば、κ(a)はほぼ角度 φ (a, b)に比例します。
この考え方を曲面(実際にはポリゴンモデル)の場合に拡張したものが、我々が新しく導入した擬似的曲率で、トロピカルアングル (tropical angle of curvature) と呼んでいます。より詳細な技術の説明は論文[3] をご参照ください。トロピカルアングルによる複数スケール毎のエントロピー計算は、大規模ポリゴンに対しても安定した結果を提供することが確認できました。以上により技術課題の (1) は達成する見込みがたちました。
残る 技術課題 (2) と (3) をクリアする工夫の概要は以下の通りです。
本手法では、適応的なサブサンプリングアルゴリズムを導入し、誤差をほとんど発生させずに、3桁までのスピードアップを可能にしました。さらにIMAGICA GROUP内での実験をベースにして GUIを改良しつつ、アーティストが直感的に指示しやすいパラメータを提供できるようになりました。図5に示したような GUIを提供することで、アーティストは1〜5個のパラメータを用いた対話処理により、所望の結果を求めることができます。これらの高速化とGUIに関する技術の詳細は、論文[3] をご参照ください。
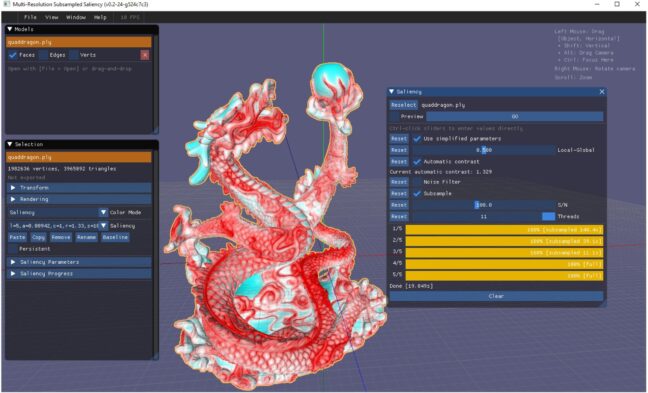
図5 対話型 GUIの実装.アーティストは微調整を含めて最大5つのパラメータで制御可能.
本手法では、例えば数百万ポリゴン以上の高密度ポリゴンモデルに対しても、安定かつ高速な計算を保証し、実験では従来の手法に比べて最大で3桁の高速化を達成しました。アーティストによる評価でも、実データに適用可能であることを確認しています。
今後、ボリューメトリックキャプチャー(volumetric capture) からのポリゴンモデル生成や点群データ (point-cloud) からのポリゴンモデルの需要が急拡大することが見込まれます。
ポリゴン削減は、データ軽量化やリアルタイム/高速表示を可能にするための必須技術でありますので、引き続き様々な応用分野を見据えて研究開発を進めていく予定です。

図6 本手法によるポリゴン削減結果
動画
[4] 安生健一, “CGは数学でできている -映像数学の展望”, 日本評論社, 2023
映像表現の最先端で一緒に働きませんか?
研究開発に興味をお持ちの方、
実現したい何かをもつ方、映像分野が好きな方はぜひご応募ください。
誰も見たことのない未来をともに創り出すメンバーを待っています。

▶︎IMAGICA GROUP アドバンストリサーチグループ 採用情報はこちら
ARGおよびグループ会社と共同開発・研究を行ってみたい
大学研究室や企業研究所を募集しております。
ご興味がある方は、以下のフォームよりお問い合わせくださいませ。
「IMAGICA GROUP」が
テクノロジー×クリエイティブで目指す
イノベーションとは

視覚×コミュニケーション×AI
最先端の研究分野で化学反応を起こし、まだ誰も見たことのない映像表現を追求
奈良先端科学技術大学院大学×千葉大学×IMAGICA GROUP
顔表示に特化した
ライトフィールドディスプレイの研究
東京農工大学とIMAGICA GROUPによる、
共同研究と目指す未来
